PRINCIPIO DE HAMILTON. MECÁNICA

Introducción

En los siglos siguientes al establecimiento de la Mecánica newtoniana (XVIII y XIX), muchos fueron los autores que dedicaron su tiempo a intentar fundamentarla teóricamente, entre ellos cabe destacar a D'Alembert, Euler, Maupertuis, Laplace, Lagrange, Legendre, Gauss, Liouville, Poisson, Jacobi y Hamilton. Vamos a entender ahora alguno de estos pilares matemáticos en los que se fundamenta la moderna teoría de campos, empezando por el llamado principio de acción estacionaria o de Hamilton.

Coordenadas generalizadas

Las coordenadas clásicas de un sistema físico en un espacio N-dimensional son los vectores de posición de cada uno de sus puntos materiales, 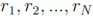, las cuales normalmente están sujetas a algunas ligaduras del tipo:

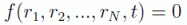
Esta clase de ligaduras o enlaces se denominan de posición u holónomas, y son las que estudiaremos con detalle en los siguientes puntos. Los sistemas con esta clase de enlaces se denominan sistemas holónomos. No existe una manera general de abordar los problemas no holónomos (habría que utilizar en este caso la técnica de los multiplicadores de Lagrange y tener en cuenta las ligaduras concretas). No obstante, a efectos de deducciones de leyes fundamentales, no se pierde generalidad al considerar que todos los sistemas son holónomos, dado que siempre se consideran sistemas de partículas y los efectos no holónomos son típicos de los sistemas macroscópicos.

Si un sistema está restringido a un conjunto de k ligaduras como la anterior en realidad sus grados de libertad efectivos no coincidirán con los físicos, y se lo podrá estudiar con menos parámetros, digamos n:

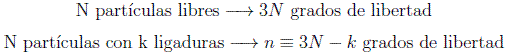
Se definen entonces unas nuevas coordenadas para el sistema, que no tienen que tener correspondencia con el espacio físico real, llamadas coordenadas generalizadas, 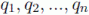, que forman el llamado espacio de configuraciones. En general para estudiar la trayectoria de un sistema físico necesitamos también conocer las llamadas velocidades generalizadas, 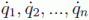, que junto con las coordenadas anteriores constituyen un conjunto de 2n variables que fue designado por Gibbs con el nombre de espacio de las fases. En este diagrama se representan las coordenadas en el eje x y las velocidades o momentos en el eje y.

Integral de acción

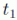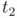Se pueden obtener las ecuaciones del movimiento de un sistema a partir de un principio que considere el movimiento entero entre los tiempos $t_1$ y $t_2$ y pequeñas variaciones virtuales del movimiento respecto al real. En un espacio de configuraciones de 2 dimensiones se vería:

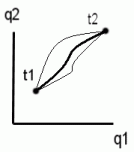
normalmente se usan q y 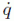$\dot{q}$ para significar los dos conjuntos de coordenadas y velocidades respectivamente.

El principio de Hamilton trata de ver cuál de todas las trayectorias q(t) es la real a partir de extremar la siguiente función integral:

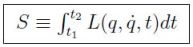
$S\equiv \int _{t_1}^{t_2}L(q,\dot{q},t) dt$

llamada integral de acción. S es una funcional que asigna un número a cada función q(t) definida en el intervalo (t1,t2). A la función L se la conoce con el nombre de lagrangiana del sistema, y es la función que debemos encontrar. La variable t juega el valor de un parámetro ya que se supone que L no depende explícitamente del tiempo.

Ecuaciones de Euler-Lagrange

Sea q(t) la trayectoria real del sistema. Entonces las trayectorias virtuales serán de la forma:

q(t)+δq(t)

cumpliéndose en los extremos de los intervalos que todas las funciones deben tomar los mismos valores:

δq(t1)=δq(t2)=0

La variación de la acción se puede poner como:

S(q+\delta q)-S(q)=\delta S+O({\delta q} ^2)=\int _{t_1}^{t_2} \delta L dt

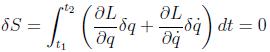
que será igual a cero si utilizamos la condición de extremal que sugiere el principio propuesto para la integral de acción:

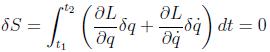
\delta S = \int _{t_1}^{t_2}\left(\frac{\partial L}{\partial q}\delta q+\frac{\partial L}{\partial \dot{q}}\delta \dot{q}\right)dt=0

integrando el segundo término por partes:

\int _{t_1}^{t_2}\frac{\partial L}{\partial \dot{q}}\frac{d}{dt}(\delta q)dt=\left[\frac{\partial L}{\partial \dot{q}}\delta q\right] _{t_1} ^{t_2}-\int _{t_1}^{t_2}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right)\delta q dt

por tanto

\delta S=\left[\frac{\partial L}{\partial \dot{q}}\delta q\right] _{t_1} ^{t_2}+\int _{t_1}^{t_2}\left[\frac{\partial L}{\partial q}-\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right)\right]\delta q dt=0

en donde el primer sumando se anula dada la condición de coincidencia en los extremos.

Como la integral debe anularse para todo valor de δq, llegamos a las ecuaciones de Euler-Lagrange, que deberá cumplir nuestra función lagrangiana:

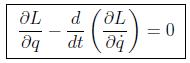
\genfrac{}{}{}{0}{\partial L}{\partial q}-\genfrac{}{}{}{0}{d}{dt}\left(\genfrac{}{}{}{0}{\partial L}{\partial \dot{q}}\right)=0

que en realidad son n ecuaciones diferenciales que establecen la relación entre las aceleraciones, las velocidades y las coordenadas, es decir, son las ecuaciones del movimiento del sistema.

Elección de la lagrangiana

Para encontrar las ecuaciones del movimiento habrá que elegir una función lagrangiana adecuada. El llamado programa de Einstein sugiere que se construya ésta a partir de las simetrías del sistema y que las cantidades conservadas y las leyes del movimiento surjan como consecuencia de éstas.

Debe señalarse que hay infinitas lagrangianas que definen las mismas ecuaciones del movimiento. En efecto, cualquier otra lagrangiana del tipo:

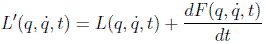
L'(q, \dot{q},t)=L(q,\dot{q},t)+\frac{dF(q,\dot{q},t)}{dt}

dará lugar a una acción que diferirá de la original en un término constante que desaparecerá al hacer la variación:

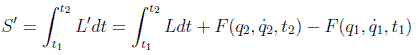
S'=\int _{t_1}^{t_2}L'dt=\int _{t_1}^{t_2}Ldt+F(q_2,\dot{q}_2,t_2)-F(q_1,\dot{q}_1,t_1)

En general pues haremos consideraciones de simetría. Para, por ejemplo, la lagrangiana de una partícula libre se supone que el tiempo es homogéneo y que el espacio es homogéneo e isótropo. De esta forma la lagrangiana no podrá depender explícitamente de t (homogeneidad del tiempo), pero tampoco podrá depender de r (homogeneidad del espacio) ni de la dirección de v (isotropía del espacio). Será por tanto una función proporcional al cuadrado de la velocidad. Por razones históricas se suele llamar T y expresar como:

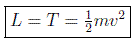
$L=T=\frac{1}{2}mv^2$

Cabe hacer notar que la multiplicación de la lagrangiana por una constante arbitraria no afecta a las ecuaciones del movimiento sino sólo a una arbitrariedad natural en la elección de las unidades de medida, en este caso de la masa. Pero los cocientes de las masas de las distintas partículas, que son los únicos que tienen sentido físico real, permanecen invariables.

Esto ocurre así incluso para un sistema de partículas, en donde la propiedad de aditividad de la lagrangiana consiste en admitir que las partes de un sistema que no interactúan con otras no pueden contener magnitudes pertenecientes a esas otras. Así para dos partículas tendríamos:

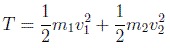
$T=\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2$

Las consideraciones de simetría las hemos realizado en función de las coordenadas físicas. En función de las coordenadas generalizadas, dado que para una partícula:

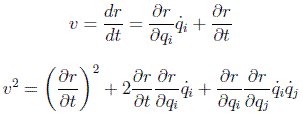
$v=\frac{dr}{dt}=\frac{\partial{r}}{\partial{q_i}}\dot{q}_i+\frac{\partial r}{\partial t}$

en donde se usa el convenio de Einstein de suma sobre índices repetidos. Definiendo:

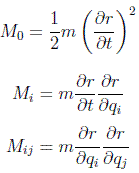
momentos

se puede poner la lagrangiana libre como:

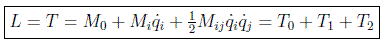
$L=T=M_0+M_i\dot{q}_i+\frac{1}{2}M_{ij}\dot{q}_i\dot{q}_j=T_0+T_1+T_2$

es decir, como suma de tres funciones, independiente, lineal y cuadrática respectivamente en relación con las velocidades generalizadas.

Cuando las ecuaciones de transformación no dependen explícitamente del tiempo (ligaduras esclerónomas), T será siempre una forma cuadrática homogénea de las velocidades generalizadas.


En el caso de un sistema de partículas que interactúen entre sí se le suele añadir a la lagrangiana otra función que caracteriza las interacciones en la forma:

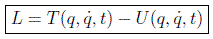
$L=T(q,\dot{q},t)-U(q,\dot{q},t)$

veremos en breve la interpretación de estas cantidades como energías cinética y potencial respectivamente.

Teoremas de conservación

Las ecuaciones de Euler-Lagrange forman un sistema de n ecuaciones diferenciales de segundo orden con n funciones desconocidas qi(t), por tanto, la solución general contendrá 2n constantes arbitrarias que se determinarán por las condiciones iniciales del sistema (teorema de Cauchy-Kowalevski). Como se supone que las ecuaciones del movimiento no dependen explícitamente del tiempo, el origen de éste es arbitrario. Por tanto, tendremos 2n-1 constantes arbitrarias, función de las coordenadas y las velocidades generalizadas. A estas constantes se las denomina integrales del movimiento o cantidades conservadas. Entre estas habrá que elegir las más relevantes atendiendo a su sentido físico, es decir, a las simetrías con las que están relacionadas.

En realidad, la mayoría de los sistemas no son integrables totalmente, pero siempre se podrán sacar conclusiones físicas importantes por consideraciones de simetría.

Cuando la lagrangiana de un sistema no dependa de una coordenada dada qi la ecuación de Euler-Lagrange correspondiente quedará:

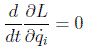
$\frac{d}{dt}\frac{\partial L}{\partial {\dot{q}_i}}=0$

a la cantidad:

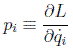
p_i\equiv \frac{\partial L}{\partial \dot{q}_i}

se la denomina cantidad de movimiento canónica o generalizada (no tiene por qué tener las dimensiones de una cantidad de movimiento clásica). Por tanto, cuando las ecuaciones del sistema no dependen de una coordenada, su cantidad de movimiento se conserva:

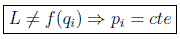
\framebox {$L\neq f(q_i)\Rightarrow p_i=cte$}

a la coordenada aludida qi se la suele denominar coordenada cíclica o ignorable.