
LOS POSTULADOS DE LA MECÁNICA CUÁNTICA

Aunque el desarrollo de la teoría cuántica se sitúa en el primer cuarto del siglo XX, iniciado en 1900 con el descubrimiento del quanto de Max Planck, no fue hasta los años 30 cuando se establecieron los principios matemáticos de la Mecánica Cuántica moderna. Estos principios se relacionan fundamentalmente con los trabajos de Born, Dirac y, sobre todo, John von Neumann (1932).
La axiomatización dada por von Neumann perduró durante más de medio siglo en la mayoría de los libros clásicos de Mecánica Cuántica. Sin embargo, en los años 90 la mayoría de los físicos empezó a adoptar una actitud crítica hacia esa forma de postulación, especialmente en lo que concernía al desarrollo intuitivo de la misma y, sobre todo, al tratamiento que se hacía del problema del colapso de la función de onda.
En efecto, a pesar de que en los textos clásicos se parte del concepto de estado para pasar luego al de observable incluyendo como postulados el colapso, la evolución temporal y las relaciones de incertidumbre, una visión más moderna consiste en partir del concepto de observable suprimiendo los tres últimos postulados a los que se llegará por diferentes consideraciones, y manteniendo sólo el postulado de supersposición de estados y el de Born acerca de la interpretación probabilística. Una visión más cercana a ésta última será la que adoptemos en estos apuntes.
No obstante, hay que remarcar que las conclusiones experimentales a las que se llega con cualquier conjunto de axiomas que se puedan elegir son, y de hecho deben ser, exactamente las mismas, no tratándose esto, en mi opinión, más que de una mera cuestión formal. De hecho para la mayoría de los físicos, que no trabajan en los fundamentos de la Mecánica Cuántica, es esta una cuestión transparente.
Cada sistema cuántico se estudiará con un espacio de Hilbert H complejo, separable y equipado.
Al margen de consideraciones topológicas, un espacio de Hilbert separable es un espacio vectorial V en donde se puede definir un producto escalar y una base lineal finita o infinita numerable (base de Hamel).
El concepto de equipación del espacio se escapa de los objetivos de estos apuntes. Baste decir que se puede consultar en los trabajos del matemático ruso Israel Gelfand y que nos permitirá incluir una serie de funciones generalizadas debidas a Dirac.
Según esta notación, los vectores de H se llaman vectores ket y se denotan con |Ψ >. También se define un espacio dual H', isomorfo al anterior, en el que cada vector de H es tratado como un funcional lineal Φ de H' de tal forma que a cada elemento de H le asocia un escalar. A estos vectores se los denomina vectores bra, y se denotan como <Φ|:

y, lógicamente, en esa definición se asume que se usará el producto escalar definido en cada espacio de Hilbert.
Habitualmente en espacios discretos los vectores ket son vectores columna y los vectores bra son vectores fila. En ese sentido, se puede ver que, así como un ket por un bra es un c-número o simple número complejo (por usar términos de Dirac), un vector ket por un bra será un q-número u operador, y si ambos coinciden en el primer caso obtendremos la unidad y en el segundo el proyector sobre ese vector.
En cada espacio de Hilbert podemos definir una base ortonormal | i > de forma que < i | j >=δij, usando la delta de Kronecker o de Dirac dependiendo del caso discreto o continuo.
Con esta base podemos definir la relación de completitud o de cierre del Hilbert usando la descomposición de la identidad
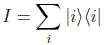
de modo que cualquier vector arbitrario |v > del espacio pueda desarrollarse en esa base:
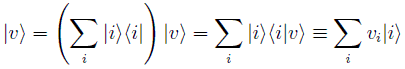
Sobre los vectores del espacio de Hilbert definiremos operadores lineales A, que cumplen:
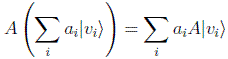
y que normalmente usaremos por medio de sus representaciones matriciales en cada base:
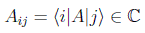
La traza de un operador lineal en una base dada será pues:
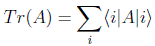
Cuando al aplicar un operador sobre un vector obtenemos:
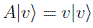
diremos que |v > es autovector de A con autovalor v. Es conocido por álgebra que los autovalores se hallan igualando a cero el llamado polinomio característico P(v)=|A-vI|=0, que no depende de la representación elegida.
El operador tendrá una representación diagonal en sus autovectores ortonormales, si los hubiera:
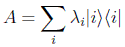
Se define el operador adjunto A+ de A a aquel que cumple:
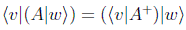
Un operador es hermítico o autoadjunto cuando coincide con su adjunto (ejemplos claros son los proyectores o la identidad). Es muy fácil demostrar que los autovalores de un operador autoadjunto son reales.
Un operador U es unitario si se cumple que U+U=I, lo que implica también que UU+=I. Estos operadores son isometrías, es decir, conservan los productos escalares y son por tanto los indicados para describir las evoluciones reversibles:
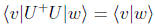
Los operadores unitarios y autoadjuntos forman parte de un conjunto mayor, los operadores normales, que cumplen N+N=NN+.
Los operadores normales tienen la particularidad de que siempre se puede encontrar una base de autovectores ortonormal, es decir, serán diagonales en esa base. Esto constituye un teorema de descomposición espectral que por su importancia vamos a demostrar a continuación.
Teorema de descomposición espectral
Cualquier operador normal N sobre un espacio de Hilbert H es diagonal respecto a alguna base ortonormal de H
Dem: El hecho de que un operador con representación diagonal es normal es muy fácil de demostrar, así que nos vamos a detener en la demostración de la implicación directa, es decir, vamos a probar que cualquier operador normal tiene una representación diagonal.
La demostración se suele hacer por inducción sobre la dimensión del Hilbert. Para dimensión 1 es trivial, ya que todos los operadores, lógicamente, son diagonales.
Hay que probar por tanto que si se cumple para n-1 se cumplirá para n. Para eso vamos a intentar descomponer el operador N. Si suponemos que P es el proyector sobre el subespacio de uno de los autovalores de N y Q el proyector complementario, es obvio que P+Q=I. Por tanto podemos poner:
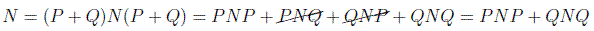
Debemos justificar esas dos cancelaciones. Que QNP es nulo es evidente, dado que P sobre un vector por la derecha proyecta sobre el subespacio de autovalores de N y Q es justamente el proyector ortogonal que anularía todo.
Para la anulación de PNQ hay que hacerlo actuar sobre un vector por la izquierda, y se llega a la misma conclusión que en el caso anterior, P y N dejarán al vector en el subespacio ortogonal a Q.
Por último, si probamos que QNQ es normal, como se aplica al subespacio restringido de dimensión n-1, habrá que admitir que es diagonal por el principio de inducción, y es obvio que PNP ya es diagonal sobre cualquier base que contenga al vector perteneciente a P. Para probar lo primero usamos el hecho de que N es normal, que Q2=0 y la identidad QN=QN(P+Q)=QNQ y tenemos que QNQQN+Q=QNQN+Q=QNN+Q=QN+NQ=QN^+QNQ=QN+QQNQ, luego QNQ es normal y ya estaría demostrado el teorema.
De aquí se deduce que todo operador normal, o autoadjunto, o unitario, se podrá siempre descomponer en términos de sus autovectores o de los proyectores ortogonales sobre los mismos en la forma:
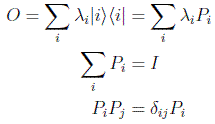
siendo |i > la base de autovectores con los autovalores λi y Pi los proyectores sobre los subespacios de autovalor λi.
Un estado es representado por un operador ρ, también llamado matriz densidad, no negativo, autoadjunto y de traza unidad. Los observables también serán operadores autoadjuntos, y sus autovalores serán los posibles valores de las magnitudes físicas.
El hecho de que el operador estado sea autoadjunto nos garantiza que se puede descomponer en una representación espectral de la forma:
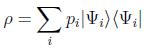
en términos de sus autovalores y autovectores ortonormales, en donde hemos supuesto un caso discreto por conveniencia.
Aparte por las condiciones del postulado se debe cumplir:
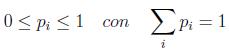
llamándose este tipo particular de combinación lineal combinación convexa.
Dentro de los estados mezcla se encuentra el caso particular de los estados puros:
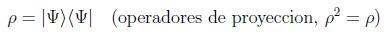
A menudo se asocia en este caso el estado del sistema no con su matriz densidad sino con el llamado vector estado |Ψ > que al ser un rayo unidad en el espacio de Hilbert tendrá una ambigüedad de fase y existirá la equivalencia:
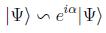
Sin embargo, el operador estado es independiente de esta fase arbitraria. Además, se puede probar como teorema que estos estados puros no pueden ser representados por combinaciones convexas de otros estados, al contrario que los estados mezcla estricta.
Hay que destacar que la representación de un estado no puro como combinación convexa de estados puros no es única y depende de la base que utilicemos, que no tiene por qué ser siempre la base de autovectores ortonormales.
Como ejemplo, en un espacio de Hilbert de dimensión 2, sea un estado no puro preparado en los estados puros no ortogonales:
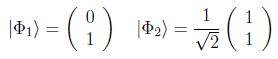
de la siguiente forma:
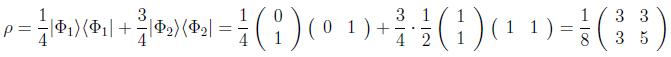
pero también podemos hacer otro desarrollo calculando sus autovectores y autovalores, obteniendo:
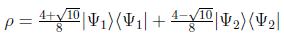
en donde se han usado en este caso los autovectores ortonormales:
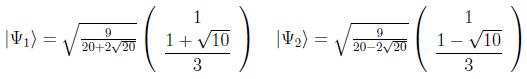
Vamos a demostrar dos teoremas relativos a las propiedades de los operadores que nos serán de mucha utilidad.
Teorema 1
Si A y B son dos operadores autoadjuntos que poseen un conjunto completo de autovectores y que conmutan (es decir [A,B]=AB-BA=0), existe un conjunto completo de autovectores de ambos.
Dem: Sean los dos conjuntos de autovectores:
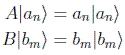
Se puede desarrollar |an > en la base de autovectores de B y haciendo uso de la definición de autovector obtendríamos:
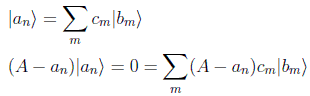
Si se anularan todos los términos por separado tendríamos demostrada una implicación, ya que |bm > sería también autovalor de A. Para que se anulen todos los términos del sumatorio por separado debemos demostrar su independencia lineal. Si operamos con B por la izquierda y usando la conmutatividad en cada término del sumatorio obtenemos:
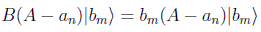
es decir, (A-an)|bm > es autovector de B con autovalor bm, y por tanto todos los términos del sumatorio serán ortogonales y se tendrán que anular por separado, lo que quiere decir que |bm > también será autovalor de A.
Con un sencillo cálculo algebraico obtendríamos la implicación inversa y concluiría la demostración.
Esto se puede ir haciendo para el resto de operadores conmutantes que encontremos. En general el grupo de estos operadores en el que no hay degeneración (para cada autovalor existe un único autovector) se denomina conjunto completo de operadores que conmutan.
Teorema 2
Cualquier operador que conmute con un conjunto completo de operadores que conmutan será función de los operadores de ese conjunto.
Dem: Sea el conjunto (A,B,...) de operadores con autovectores |an,bm... >:
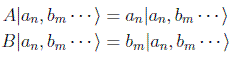
y sea F el operador que conmuta con todos ellos. Por el teorema anterior ahora el conjunto completo sería el ampliado (A,B,...,F). Pero los vectores |an,bm ... > son los únicos autovectores del conjunto completo en ese espacio de Hilbert, luego deben ser también autovectores del ampliado:
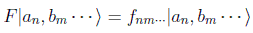
y por tanto debe haber una función tal que:
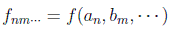
El valor medio de una variable dinámica O (que puede representar un observable) en el conjunto de estados igualmente preparados representados por el operador ρ es
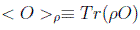
y nos dará también la distribución de probabilidad de esa variable en la base del espacio de Hilbert considerada.
Vamos a ver la expresión general que tiene el valor medio de un observable por medio de cierta base ortonormal:
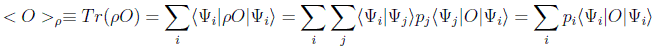
y lógicamente si estuviéramos en el estado puro representado por el vector |Ψ > el valor medio se reduciría a:
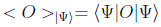
es decir, se puede decir en general que el valor medio del observable en un estado cualquiera es el promedio estadístico de sus valores medios en cada estado puro y cuyos pesos son precisamente los coeficientes de la descomposición convexa del estado en esa base.
Sea A un observable, supongamos que de espectro discreto (el caso continuo es muy parecido), en su descomposición espectral de autovectores:
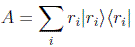
Si quisiéramos estudiar una función de ese observable, es asumible pensar que podríamos usar esta descomposición. Podemos utilizar la función de Heaviside (o función escalón):
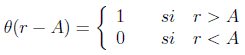
Vamos a preguntarnos por una densidad de probabilidad g(r), que nos daría la probabilidad de encontrar al sistema con un valor del observable en el intervalo [r,r+dr] en un estado arbitrario ρ. Entonces la probabilidad de que el observable A tuviera un valor menor que r sería:
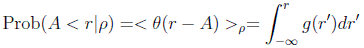
pero por otra parte, por el tercer postulado y las consideraciones hechas arriba:
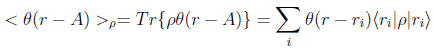
luego, igualando
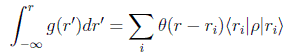
es decir
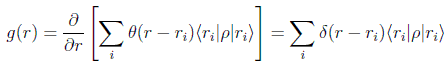
lo que indica que los únicos valores de probabilidad no nula son los autovalores del observable.
Vamos a preguntarnos ahora por la probabilidad de que se obtenga un valor arbitrario r de ese observable en el estado ρ:
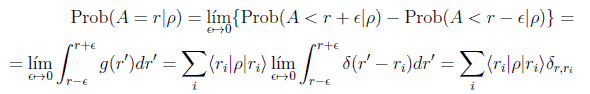
Usando el operador proyección sobre el subespacio de autoestados con autovalor ri=r:
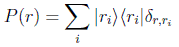
con el que, usando la propiedad cíclica de la traza, obtenemos la expresión general para la probabilidad:
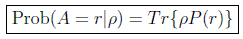
en donde se pueden ver los dos factores en juego, el estado del sistema y el filtro correspondiente al valor concreto del observable.
En el caso particular de un estado puro ρ=|ψ >< ψ| se obtiene la expresión:
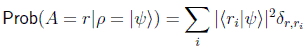
y si lo que queremos comprobar es un autovalor no degenerado r=ri tenemos la conocida expresión:
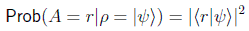
Hay que hacer notar en este último caso que la probabilidad sería la certeza absoluta en el caso de que se esté en un estado autovector del observable y se quiera medir el correspondiente autovalor, y nula en el caso de que estemos en otro estado puro ortonormal.